Power Sensor Calibration System Doubles as SWR and Return Loss Measurement Method: Part I

TEGAM, Inc.panding the use of in-house power sensor calibration system, companies can save money by avoiding additional single-use test equipment.

By John Swank, <%=company%>

Contents
Calibration system operating principles
Calibration and mismatch error
Basic SWR measurement techniques

This configuration is a type of scalar system that can be used for measuring SWR. The open circuit, short circuit and matched impedance are connected to the test port (lower leg) of the SWR/return loss Bridge for calibration purposes, before measuring the DUT.

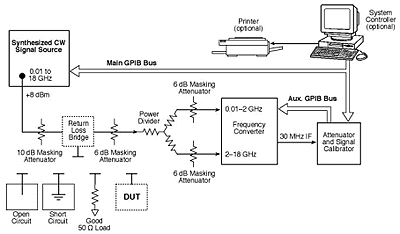
Both SWR (standing wave ratio) and return loss are a measure of the divergence of a microwave device from a perfect impedance match, for example, 50 W. These parameters are mathematically interchangeable and result from scalar measurements, which may be required for a number of reasons. For instance, it is necessary to make sure that the devices under test (DUTs) meet their specifications—one of which is SWR. Also, modern measurement practices dictate the calculation of a quantitative accuracy value, which is affected by SWR at the port of a microwave device.

There are some obvious ways to measure SWR, such as a network analyzer. However, some less obvious ways may offer advantages, such as:

1. Measuring SWR when a direct reading instrument is not available
2. Obtaining results with traceable accuracy
3. Employing the same equipment and test setup used in other measurements on the DUTs

The method described below uses a power sensor calibration system for SWR/return loss measurements. It is a scalar measurement system whose principal function is power sensor calibration. However, when combined with a return loss bridge, it can be used to characterize the SWR performance of passive devices or sensors. Thus, expanded use of this system eliminates the need to purchase separate equipment for SWR measurements.

top
Calibration system operating principles
A power sensor calibration system functions by providing a precisely known source of power, which is then measured by the sensor under test. The ratio of the measured value of power to the known value is the calibration factor, K₁, of the sensor. This is shown mathematically as follows:

where: P_m is the power indicated by the sensor/power meter, and
P_rf is the actual power from the precision source.

The calibration system itself has to be calibrated against a common standard to provide consistency in measurements. This is termed traceability, and is provided by having a traveling standard, a terminating mount, calibrated by the National Institute of Standards and Technology (NIST) or other calibration laboratories. This traveling standard is then used to measure the power emanating from the power source in the calibration system.

top
Calibration and mismatch error
Every calibration has associated with it an uncertainty value, which takes into account the inaccuracy and drift of all the instruments and devices used in the calibration. Accuracy is affected by connector repeatability, temperature stability of the thermistor mount standard, etc. A major source of error in any transfer of power from one instrument to another is due to mismatch. This can cause large errors, especially at higher frequencies.

Modern measurement techniques require these uncertainties to be calculated for each calibration point, and the values inserted into a measurement results report. To do this, sources of measurement error must be defined quantitatively. Typically, calibration software is used to calculate uncertainty values using measurement data files, etc.

The maximum error due to mismatch can be deduced from the SWR values of the two instruments or devices being connected together. The two devices in this case are the sensor being calibrated and the precision source, e.g., a feedthrough mount. Each of these devices has a specified maximum SWR. Table 1 lists the SWR specifications for a sensor and a feedthrough mount at various frequencies. The calculated maximum mismatch error induced in a transfer of power from one to the other is shown in the last column.

In general, maximum mismatch error, M, can be calculated from the following equation:

where |₁| and |₂| are the magnitudes of the reflection coefficients of the two impedances involved. || is related to SWR by the following equation:

,

where S is the SWR.

From these equations it can be seen that the lower the reflection coefficient, and hence the SWR, the lower the potential mismatch error during power transfer from one device to the other. Since SWR is a scalar quantity, it can only be used to estimate the possible error in the transfer. If actual SWRs are not known, the devices' specified SWRs can be used in the equation, under the assumption that they meet their specifications. However, if the actual SWR of even one of the devices is known, then a (presumably) reduced value of estimated maximum mismatch error can be calculated.

Users of power standards might have full "S" parameter data in the form of a published report that comes with the system. The only unknown should be the SWR of the sensor under test.

top
Basic SWR measurement techniques

Figure 1 Caption: The configuration shown in Figure 1 is the type of scalar system described earlier that can be used for measuring SWR. The open circuit, short circuit and matched impedance are connected to the test port (lower leg) of the SWR/return loss Bridge for calibration purposes, before measuring the DUT.

Figure 2 Caption: A measurement configuration similar to that used for a sensor calibration is shown here for a terminating type sensor. Calculation of the sensor calibration factor, K1, was described earlier in the section on Calibration System Operating Principles.

Figure 3 Caption: This setup is similar to Figure 2 but with a SWR/return loss bridge connected between the precision source output and the sensor being "calibrated." In this setup, two different "calibrations" are performed. First a short or open is connected to the test port of the SWR bridge. This has the effect of reflecting all of the power from the precision source through to the sensor. The DUT is then connected to the test port of the SWR bridge and a second calibration of the sensor performed. In this case only a portion of the power is reflected from the device under test through to the sensor. The ratio of the powers is the return loss of the device under test.

Results from the various test setups can be expressed mathematically as follows:

Case 1. Total power is reflected from the short/open.

where P_rf is the power emanating from the precision source, P_mr is the power registered by the power meter attached to the terminating sensor, and K_1r is the calibration factor of the sensor.

Case 2. The DUT is attached to the bridge test port.

where P_mt is the power as now registered by the power meter attached to the terminating sensor, and K_1t is the equivalent calibration factor of the sensor. (The calibration factors are denoted by K₁ as this is the normal identification of the calibration factor of a terminating sensor.)

In this measurement sequence the so-called calibration factors have little relevance to the performance of the terminating sensor. If calibration measurements are being performed by hand, all that is needed is the power meter readings. However, the calibration system software gives results in terms of calibration factors. To cover a large number of measurement frequencies, it is more expedient to use the software to generate calibration factors.

It can be seen from the equations that a calibration factor is proportional to measured power, so the two can be used interchangeably. Therefore, the return loss of the DUT is the ratio of the so-called calibration factors, i.e.,

Software for the calibration system described above was designed by TEGAM for calibrating sensors. This technique for measuring SWR makes use of that software. However, the current version of the software does not automatically calculate the calibration factor ratios, or perform other math functions associated with SWR measurements. At present, this is a manual task.

Still, the software can perform the averaging of the "Open" and "Short" reference measurements by calling up two runs, with a pause between the two, as required for testing connector repeatability. After the first run with an "Open" attached to the return loss Bridge, the software will wait while the "Short" is attached. The final set of results will be the average of the two measurements (Reference 3).

To Be Continued

References

1. "100 mW Feedthrough Power Standard," Application Note #212 from TEGAM.
2. "System IIA, Automatic Power Meter Calibration System," Manual IM-198, from TEGAM, section 3-10
3. "System IIA Software Operations," Manual IM-235, from TEGAM, section 2-3.5.1.

top
Next week, TEGAM's John Swank will continues his discussion of how to conduct SWR and return loss measurements through power sensor test setups that reduce the need for additional test equipment for devices under test.